

 |
Rotation of x,y,z about fixed point O, referred to fixed axes X,Y,Z
can be described completely by keeping track of the angular positions α,
β, θ. For example, assign unit vectors to the positive directions as follows: êx, êy, êz in positive directions of X, Y, Z and îx, îy, îz in positive directions of x, y, z. Then îx = cos(x,X)êx + cos(x,Y)êy + cos(x,Z)êz, îy = cos(y,X)êx + cos(y,Y)êy + cos(y,Z)êz, îz = cos(z,X)êx + cos(z,Y)êy + cos(z,Z)êz. |
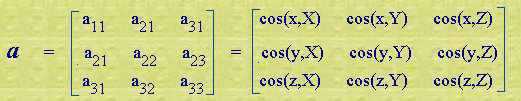
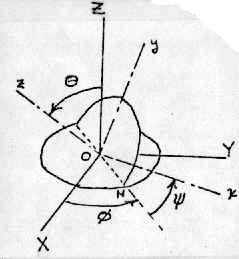 |
Line ON is called the line of nodes. The position of axes x, y, z can
be thought of as having been obtained by the following sequence of
rotations: 1. rotation through φ with OZ fixed, 2. rotation throuth θ about the line of nodes, 3. rotation through ψ with Oz fixed. |
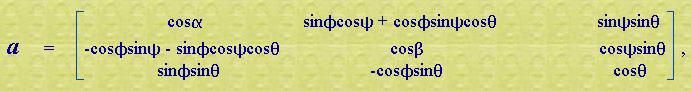
If the case where sinθ = 0 is treated separately, and α, β, θ are considered as known angular coordinates, then Euler angles φ, ψ can be calculated with aid of the formulae φ = (cos-1(c + d) + cos-1(c - d))/2 and ψ = (cos-1(c -d) - cos-1(c + d))/2, where c = cosα + cosθ(cosαcosθ - cosβ)/sin2θ and d = (cosαcosθ - cosβ)/sin2θ. Thus, when α, β, θ are given, Euler angles φ, ψ can be calculated, and off-diagonal elements a12, a13, a21, a23, a31, a32 can in turn can be calculated in terms of θ, φ, ψ. I think of given angles α, β, θ as equations of right cylindrical cone sheets, with axes X, Y, Z, respectively; and apices all at the origin O. With this interpretation, rotated body axes x, y, z are particular generators of the cones, such that unit vectors îx, îy, îz define an orthogonal triad. It is not alwats possible to meet the orthogonality conditions for arbitrarily chosen α, β, θ. Whatever α, β, θ values are assigned, the rotation is only proper when the determinant of direction cosine array a satisfies the condition deta = |a| = 1. Six of 33 original pages of the rotation notes have been transcribed. |
| One of the assignments I was given while
working at the Lockheed-California Company was to direct research at the
Research and Development Center outdoor Antenna Test Laboratory.
 I wrote a technical paper to summarize applications of my rotation theory. The title: "Body Angles and Rotation Arrays in Forth, by Glenn E. Bowie". |

 |
  |